Raster-Koordinaten: ein neues, einzahliges Koordinatensystem
Autor und Erfinder: Leonhard Heinzmann Stand: 2. 4. 2008
Kurzbeschreibung
Raster-Koordinaten sind ein neuartiges Koordinatensystem.
Die Positionsangabe (auch in der Ebene oder im n-dimensionalen Raum)
besteht nur aus einer Zahl! Trotzdem ist dieses System ergonomisch,
d.h. vom Menschen leicht als Position interpretierbar.
Beispiel: ein Koordinatensystem der Ebene
Angenommen, wir wollen die Position eines Objekts auf einer Karte angeben.
Dazu teilen wir die Karte zunächst in 3*3 numerierte Quadrate:
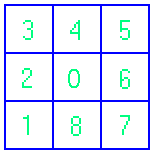
Position 0 bedeutet nun, daß das Objekt etwa im Zentrum der
Karte liegt. Position 3 bedeutet, daß das Objekt in Quadrat 3 liegt.
Diese Positionsangabe ist für ein Gebirge genau genug. Was aber tun
wir, wenn wir z.B. die Position einer Stadt genauer angeben wollen?
Ganz einfach: wir unterteilen jedes der 9 großen Quadrate wieder
in 9 kleinere, genauso numerierte Quadrate:
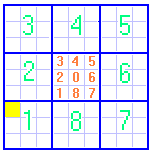
(Aus Platzgründen fehlt im mittleren großen Quadrat die grüne Ziffer 0,
in den anderen großen Quadraten die Numerierung der kleinen Quadrate).
Nun bedeutet z.B. Position 1,3 [1 Komma 3]: "Im großen Quadrat 1 das
kleine Quadrat 3" (im Bild gelb markiert).
Wir benutzen das Dezimalkomma, um anzuzeigen, daß die neuen Quadrate
Bruchteile der ursprünglichen sind. Die Größe der alten Quadrate
nehmen wir als Grundeinheit. Die Grundeinheit ist also eine Fläche!
Die Ortsangabe (Koordinate) 0 bedeutet "im Quadrat 0", beeinhaltet
also eine gewisse Unschärfe! Diese Unschärfe läßt sich durch
Nachkommastellen beliebig verringern, bleibt aber immer größer als 0.
Doch was tun wir, wenn wir die Karte erweitern wollen? Ganz einfach:
Wir verneunfachen den ursprünglichen Block aus 9 großen Quadraten,
indem wir ihn mit 8 gleichen Blocks umgeben (große Ziffern):
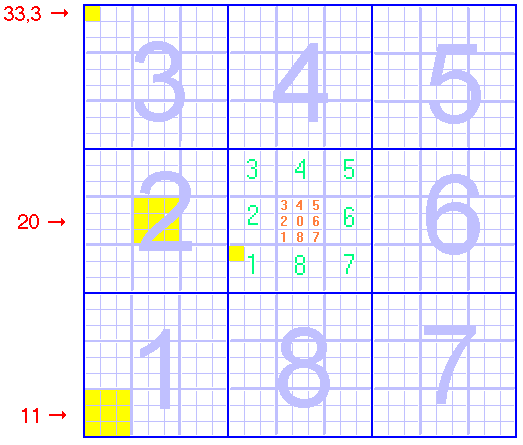
(Aus Platzgründen fehlt im mittleren Quadrat die große Ziffer 0,
in den anderen großen Quadraten die Numerierung der kleineren Quadrate).
Die Positionsangabe / Koordinate hat jetzt 2 Ziffern vor dem Komma (doch kann
man führende Nullen weglassen).
Z.B. bedeutet Position 01,3 (oder 1,3) wie im vorigen
Bild das gelbe Quadrat im mittleren großen Quadrat 0. Position 33,3
bedeutet das gelbe Quadrat links oben. Position 11 bedeutet das gelbe
Quadrat links unten, Position 20 das gelbe Quadrat in der Mitte des
großen Quadrats 2. (Die beiden letzten Quadrate haben Einheitsgröße,
sie entsprechen einer Zahl ohne Nachkommastellen.)
Man könnte eine Positionsangabe als Pfad interpretieren. Z.B. bedeutet
Position 56,7: "Gehe zu Quadrat 5 der Größenstufe 2 (weil 2. Ziffer vor
dem Komma), gehe innerhalb dieses Quadrats zu Quadrat 6 der
nächstniederen Größe, gehe dann innerhalb des letzteren Quadrats
zu Quadrat 7 der nächstniederen Größenstufe".
Man sieht: Die adressierbare Fläche wächst mit jeder weiteren Ziffer
schnell, weil exponentiell. Bei 8 Ziffern hat das adressierbare
Quadrat die Seitenlänge 38 = 6561 Urquadrate.
Richtungsangabe

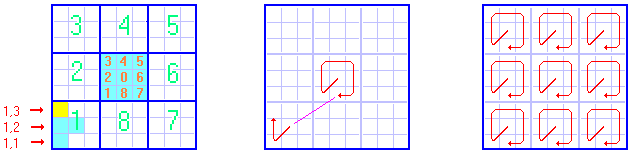
Die Numerierung der 9 Quadrate (Bild links) definiert offensichtlich einen
Drehsinn (Bild 2, innen), wenn man die Ziffern in Reihenfolge ihres Werts liest,
und ein Richtungssystem (Bild 2, Striche außen): Koordinatenursprung ist
Quadrat 0, den Quadraten 1 - 8 entsprechen 8 Hauptrichtungen.
Die ungeraden Ziffern (die Ecken des Quadrats) entsprechen
den Diagonalen (Bild 3), die geraden Ziffern (das Mittelkreuz des
Quadrats) den senkrechten / waagrechten Richtungen (Bild rechts).
Generell gibt die erste Zahl einer Positionsangabe immer die Hauptrichtung
an, in der ein Quadrat liegt.
Bei den folgenden Ziffern wird's umständlich. Zwar bedeutet eine Folge
gleicher Ziffern (mit beliebigen Nullen) in einer Positionsangabe,
daß das gemeinte Quadrat - vom Urquadrat 0 aus gesehen - genau in
einer der 8 Hauptrichtungen liegt. Z.B. liegen die Quadrate 444, 440, 404, 400
und 44,4 (44 Komma 4) genau 'nördlich' von Urquadrat 0.
Quadrat 000 oder 00 oder 0 ist eben das Ursprungsquadrat.
Doch die Umkehrung gilt nicht: auch die Quadrate 48, 484 und 488 z.B.
liegen, vom Quadrat 0 aus gesehen, genau in derselben Richtung.
Joker-Zeichen
Wie in der EDV könnte man Joker-Zeichen (wildcard characters) einführen,
um ganze Gruppen von Quadraten auszuwählen:
22a wären dann per Definition alle Quadrate von 220 bis 228.
Und 1a5 wären die Quadrate 105, 115 ... 185.
Statt der Symbolziffer a für "alle" könnte man auch n für "irgendein" Element
verwenden: 22n wäre dann irgendeins der Quadrate zwischen 220 und 228.
Obige Gruppenauswahl mit 'a' läßt sich auch so erzielen:
Man ersetzt in der Numerierung eines Neunerblocks von Quadraten
die Ziffer 0 durch 9. Die Null kann man jetzt dazu verwenden,
größere Quadrate anzusprechen:
10 wäre die Gesamtfläche des Quadrats 1 der Größenstufe 2,
100 die Gesamtfläche des Quadrats 1 der Größe 3.
Da aber beim Durchlauf der Zahlen 1, 2 ... 10, 11 ... die definierten
Quadrate verschieden groß sind, und sich die größeren mit den kleinen
überlappen, ist diese Art der Adressierung für math. Funktionen
(Funktionswert = Höhe eines Quadrats) unbrauchbar.
Außerdem hätte dann das Urquadrat viele Adressen, nämlich 9, 99, 999 ... ,
abhängig von der Anzahl der umgebenden "Gürtel" aus Quadraten.
Rasterkoordinaten für Linien und Räume
Obiges Verfahren - mehrfache Unterteilung einer Einheit in Untereinheiten
und deren fortlaufende Numerierung - läßt sich auf beliebige
n-dimensionale Räume übertragen. Im 3-dimensionalen Raum sieht das so aus:
Ein Würfel (statt eines Quadrats) definiert den Koordinatenursprung und
die Maßeinheit. Um diesen Würfel legt man 26 weitere Quadrate: man
erhält so einen größeren Würfel, der aus 27 = 3*3*3 Quadraten besteht.
(Man könnte diese 27 Würfel mit den 26 Buchstaben des internationalen Latein-ABC
benennen, plus dem Leerzeichen für den mittleren Würfel.
Jeder Buchstabe gibt also eine Position im Raum an).
Im nächsten Schritt legt man um diesen Würfel wieder 26 ebensolche Würfel.
(Die Positionsangabe besteht nun aus 2 Buchstaben / Leerzeichen.)
Das Verfahren läßt sich endlos fortführen. Ein ganzes Buch läßt sich
also leicht als eine Position (ein Einheitsquadrat sehr weit vom
Nullpunkt entfernt) ausdrücken (Groß-/Kleinschreibung, Satzzeichen,
Seitenumbruch nicht berücksichtigt).
Statt Buchstaben lassen sich natürlich auch Ziffern im 27er-System
verwenden, oder je 3 Ziffern des 3-er Systems, je 1 für Länge, Breite, Höhe,
oder je 2 Ziffern des Dezimalsystems.
Werden Stufenkoordinaten für gerade Linien benutzt, ist der Unterschied
zur üblichen Zahlengeraden gering: Nur die unscharfe Positionsangabe
- Intervall statt Punkt - ist immer da. Jedoch ist es möglich
(z.B. zu kryptographischen Zwecken), die
einzelnen Abschnitte zu verwürfeln, z.B. statt 0,1,..9 die
Reihenfolge 5,1,7,4,2,8,6,3,9,0 zu verwenden. Auch lassen sich u.U.
gewundene Linien aufgrund irgendwelcher Kriterien (z.B. Minima, Maxima)
in geeignete Abschnitte unterteilen, die nicht gleichgroß sein müssen.
Verwendung: Darstellung des Zahlenraumes
Ähnlich wie die bekannte Zahlengerade, ist ein Raster-Koordinatensystem
eine geometrische Darstellung der Zahlen. Aber auf der Zahlengeraden
werden Zahlen durch einen Punkt repräsentiert, in einem Raster-Koordinatensystem
(egal ob 1-, 2-, 3- oder n-dimensional) durch einen Ausschnitt
(von Linie, Fläche oder Raum), der zwar beliebig klein gemacht werden
kann, aber nie wirklich punktförmig wird.
Achtung: Das verwendete Zahlensystem muß mit dem Raster-Koordinatensystem
harmonieren, damit dieses tatsächlich alle Zahlen repräsentiert:
Die Anzahl der Unterteilungen pro Stufe muß konstant und gleich
der Basis des verwendeten Zahlensystems sein (oder eine Potenz
davon, wenn jede Rastereinheit mit mehr als 1 Ziffer numeriert wird).
Gegenbeispiel: Interpretiert man die anfangs verwendeten
Positionsangaben (mit den Ziffern 0 bis 8) als Zahlen im Zehnersystem,
werden nicht alle Zahlen repräsentiert: Dezimalzahlen,
die Ziffer 9 enthalten, fehlen. Interpretiert man aber obige Zahlen
als Ziffern im Neunersystem, so wird jede Zahl durch ein Quadrat
in der Ebene repräsentiert.
Auf der Zahlengeraden wird eine Zahl durch einen Punkt repräsentiert,
auch durch die Strecke vom Nullpunkt bis zu diesem Punkt. Ähnlich
wird im obigen Raster-Koordinatensystem eine Zahl N durch
3 Dinge repräsentiert:
1) Das Quadrat mit der Position N
Ist N ganzzahlig, so hat das Quadrat Einheitsgröße (= Größe des Urquadrats).
Ist N gebrochen, so bedeutet jede Ziffer hinter dem Komma eine
Verkleinerung des Quadrats um 1 Größenstufe. (Deshalb ist 1 ungleich
1,0: letzteres ist eine exaktere Wertangabe, was sich grafisch zeigt
durch ein kleineres Quadrat. Z.B. entspricht im folgenden Bild
unten links der Zahl 0 das blaue mittlere Quadrat, der Zahl 1 das
genauso große Quadrat mit der grünen 1, der Zahl 1,0 das zentrale
kleine Quadrat darin, der Zahl 1,3 das kleine gelbe Quadrat).
2) Die Fläche bis Quadrat N (exclusive)
Diese erhält man, indem man bis Quadrat N alle Quadrate der gleichen
Größe wie N durchläuft. Z.B. wird Quadrat 1,3 (Bild links, gelb)
durch die blaue Fläche repräsentiert, 12 Quadrate von 0,0 bis 1,2.
(Achtung: 1,3 im verwendeten Neunersystem bedeutet 1 + 3/9, also 12/9 .
Die Fläche von Quadrat 1,3 ist auch deshalb auszuschließen, weil sonst
z.B. die Fläche bis Quadrat 1,33 incl. (alle Quadrate von 0,00 bis 1,33),
kleiner wäre als die Fläche bis Quadrat 1,3 incl.)
3) Der Weg vom Urquadrat bis Quadrat N
Dieser ist innerhalb eines Neunerblocks spiralig,
springt dann zum Quadrat 1 der nächsthöheren Größenstufe,
verläuft ab hier wieder spiralig, usw. (Bild Mitte: Der Weg zum
Quadrat 1,3). Längere Wege sind komplizierte Gebilde, z.B. (Bild rechts)
der Weg zu Quadrat 8,8: man denke sich jede Pfeilspitze (außer der
letzten) mit der Mitte des nächsten Quadrats verbunden! Das ist in
der Ebene nicht kreuzungsfrei möglich.
Verwendung: Koordinatensystem
Der Unterschied zu den üblichen (Kartesische, Polar-) Koordinaten ist:
1) Eine Raster-Koordinate gibt die Position nicht punktgenau an,
sondern als einen Bereich.
Dieser kann aber beliebig klein gemacht werden durch
entsprechende Wahl der Maßeinheit bzw. durch Angabe von Nachkommastellen.
2) Eine Raster-Koordinate ist immer nur 1 Zahl, auch wenn eine
Position in der Ebene oder im Raum angegeben wird.
Per Raster-Koordinate kann man deshalb einen ganzen Bereich (Ebene, Raum)
nacheinander durchlaufen, indem man einfach die Position schrittweise
erhöht (z.B. um jeweils 1 oder 0,01), also ohne z.B. Zahlenpaare erst
in eine definierte Reihenfolge umrechnen zu müssen.
(Bei anderen Koordinatensystemen ist das nicht möglich:
hier sind Zahlenpaare / Zahlentripel und zum Teil auch negative Zahlen nötig).
3) Weil eine Raster-Koordinate immer nur 1 Zahl ist, kann man leicht
die Dimension der Darstellung wechseln, z.B. ein Gebilde vom Raum
auf eine Ebene oder Linie übertragen:
man wechselt einfach das Koordinatensystem, sucht die der Zahl
entsprechende neue Position und markiert diese.
Man kann sogar ein Gebilde in einem unendlichen Bereich
von begrenzter Genauigkeit (Positionsangaben haben beliebig
viele Stellen vor dem Komma, aber keine Nachkommastellen) einfach
projizieren in einen endlichen Bereich mit unbegrenzter Genauigkeit
(Positionsangaben haben die Form 0,nnn mit beliebig vielen Nachkommastellen):
Man definiert die Größe des endlichen Bereichs als 1 Grundeinheit
und setzt vor die Positionszahl ein Komma: z.B. wird aus 123 nun 0,123.
(Auch die Umkehrung ist möglich).
Man kann Dimensionswechsel und Wechsel unendlich-endlich auch kombinieren,
indem man entsprechend das Koordinatensystem wechselt und vor die
Koordinate ein Komma setzt! Z.B. wäre es theoretisch möglich (in der Praxis
Gottseidank nicht) den Weltraum in Würfel von 1 cbm zu unterteilen,
für jeden Würfel die Masse festzustellen, und diese Masse als Funktionswert
(=Höhe) über einer Strecke von 1 cm darzustellen - praktisch ohne rechnen
zu müssen.
Man kann so auch einen vierdimensionalen Raum (Zeit + 3 Raumkoordinaten)
einfach umwandeln in eine ebene graphische Darstellung.
4) Die üblichen Koordinatensysteme sind starr-geometrisch, Raster-
Koordinatensysteme eher bewegt und vielfältig, organischer, "individueller":
Es gibt viele Raster-Koordinatensysteme, die sich unterscheiden
durch die Form der Grundeinheit (Quadrat, Dreieck, Kreissegment etc.),
Anzahl der Unterteilungen pro Raster, Numerierung der Teilraster
(Lage des Nullpunkts, Drehsinn) etc.
Beispiele hier
Eine mathematische Funktion sieht je nach verwendetem Koordinatensystem
verschieden aus. Es ist nötig und sinnvoll, für bestimmte Zwecke ein
bestimmtes Koordinatensystem zu verwenden.
Ein Raster-Koordinatensystem ist sozusagen fortlaufend unterteilt in
lokale Koordinatensysteme, deshalb flexibler und für viele Zwecke
besser geeignet: z.B. kann man das Netz eines Würfels (ein z.B.
T-förmiges Gebilde aus 6 Quadraten) zunächst in diese 6 Quadrate
unterteilen, und dann fortlaufend in 9 Unterquadrate.
Auch für verzerrte und verdrehte Flächen und Räume (oder ein
topologischer Raum) und in Untersysteme geteilte Systeme
scheinen Raster-Koordinaten prädestiniert; das Problem ist
aber, zu einem realen System ein strukturgleiches Koordinatensystem zu finden.
Auch für Wettervorhersage (Darstellung drehender Wolkenwirbel, die
wieder einzelne Wirbel enthalten), biologische Systeme (Pflanzenwuchs,
z.B. Blattstellung folgt zahlenmäßigen Gesetzen) u.ä.
sind Rasterkoordinaten vermutlich anwendbar.
Auch zu Chaos-Vorgängen (der Chaos Theorie), die in der Natur häufig
sind und wo der Raum immer weiter in Unterbereiche unterteilt ist,
passen Raster-Koordinatensysteme besser als übliche Koordinatensysteme.
Entsprechendes gilt für Fraktale, immer wichtiger werdende mathematische
Funktionen, bei denen sich bestimmte Figuren ständig wiederholen bis
ins unendlich Große oder Kleine.
Verwendung: Bildrasterung, Bildkompression, Bildübertragung
Vorraussetzung dafür ist die Einbettung des zumeist rechteckigen Bildes
in ein größeres Quadrat, das sich fortlaufend in 3*3 Blocks unterteilen
läßt. Dessen Seitenlänge ist die kleinste Dreierpotenz, die größer ist
als die Bildhöhe und -Breite in Pixel.
Man kann ein Bild sehr grob rastern, indem man nur 9 Zahlen auflistet,
welche die Farbe der 9 größten Quadrate angeben. Und zwar entweder
die Durchschnittsfarbe jedes Quadrats, oder die häufigste Farbe darin, oder
einfach die Farbe des mittelsten Pixels. (Letzteres Verfahren benötigt
keine Rechnung, kann aber die Durchschnittsfarbe total verfälschen).
Listet man vor diesen 9 Zahlen noch die ursprüngliche Bildhöhe und
-Breite auf, kann man das Bild auf Originalgröße zurechtstutzen.
Der Raster wird feiner, wenn man die Farbwerte der größten 9*9 = 81
Quadrate angibt (in Reihenfolge ihrer Adressen).
Es gibt nun möglicherweise Quadrate, die vollständig
außerhalb des ursprünglichen Bildes liegen. Diese erhalten entweder
die Farbe 0, oder sie werden gar nicht aufgelistet: Man hat also
weniger als 81 Farbwerte (dieser gibt dann nicht die Farbe des
nächsten Quadrats an, sondern die Farbe des nächsten Quadrats
innerhalb des ursprünglichen Bildes).
Ähnlich ist Bildkompression möglich: Quadrate, deren Unterquadrate
alle dieselbe Farbe haben, werden mit einem Kennzeichen markiert.
Die Unterquadrate werden dann später nicht mehr aufgeführt.
Dieses Verfahren zur Bildkompression ist sehr einfach, aber wohl
nicht optimal, d.h. es liefert nicht die geringstmögliche Datenmenge.
Man kann ein Bild rastern und gleichzeitig verkleinern, indem
man sozusagen an jeder Koordinate die letzte(n) Ziffer(n) streicht und
dem so adressierten Quadrat einen Farbwert zuweist
(z.B.: 11 erhält Durchschnittsfarbe der bisherigen Quadrate 110 ...118).
Bei der Übertragung von Bildern, die mehrstufig (z.B. 3-stufig)
gerastert sind, hat man 2 Möglichkeiten:
1) Man sendet die Farbwerte der kleinsten Quadrate (i.A. der Pixel)
in Reihenfolge ihrer Adressen, baut das Bild also verwirbelt-mäanderförmig auf.
2) Man sendet zuerst die Farbwerte der Mittelpunkte der 9
größten Quadrate (also der Adressen 000, 100 ... 800),
stellt aber jeweils das ganze Quadrat in dieser Farbe dar. Danach
sendet man die restlichen der 81 Farbwerte der 2. Rasterstufe
(der Adressen 010, 020 ... 080, 110, 120 ... 780, 790).
Alle 81 Quadrate der Stufe 2 werden nun in der Farbe ihres Mittelpunkts
dargestellt. Danach überträgt man alle restlichen der 9*9*9 Quadrate
der 3. Rasterstufe (=Pixel).
Der Bildaufbau erfolgt also bei Verfahren 2) in immer feinerem Raster
(wie z.B. beim JPEG-Format). Diese Form der Übertragung ist nur dann
sinnvoll, wenn das Bild beim Empfänger langsam aufgebaut wird.
Sonst ist das einfachere Verfahren 1) vorzuziehen.
Variationen:Man kann obige Verfahren abändern und ein Bild
statt in 3*3 Blocks auch in 2*2 Blocks (oder 4*4 oder 8*8 Blocks)
unterteilen, was für Menschen weniger ergonomisch erscheint,
aber besser zum Dualsystem der Computer paßt.
Eine entsprechende Änderung ist erforderlich, wenn man 3-dimensionale
Gebilde rastern will (z.B. Hologramme oder die Belegung eines Luftraums)
oder gar 4-dimensionale Gebilde (z.B. die Belegung eines Regals oder
einer 3-dimensionalen Matrix in einem Zeitraster).
Allgemein: Obige Verfahren der Bildrasterung, Bildkompression und Bildübertragung
werden - zumindest so ähnlich - bereits in der Praxis angewandt.
Mit dem Raster-Koordinatensystem werden sie aber auf eine theoretische
Grundlage gestellt, bzw. auf eine allgemeine Basis: Man kann
Unterprogramme für Raster-Koordinaten, ähnlich wie Programme für
Halbierungssuche, für verschiedene Zwecke anwenden.
Verwendung: Kryptographie
Beispiel:
Man zerlegt eine Nachricht von 9*9*9 = 729 Zeichen in 9 untereinanderliegende
Seiten von je 9*9 = 81 Zeichen, also einen Würfel mit 9 Zeichen Kantenlänge.
Nun definiert man ein Koordinatensystem, bei dem die 27 Felder eines 3*3*3
Würfels völlig unregelmäßig numeriert sind. Liest man nun die Buchstaben
in Reihenfolge ihrer Koordinaten, so ist der Text "verwürfelt".
(Eine völlig unsystematische Umordnungstabelle für alle 729 Zeichen
ist aber noch kryptographischer.)
Mit Computerhilfe und einigem Aufwand ist der Text aber von Experten
wohl zu knacken. Folgende Maßnahmen verstärken die Kryptographie:
- Vor und nach dem Verwürfeln die Zeichen umcodieren
(Z.B. mit 2 Zuordnungstabellen. Oder nochmals mit einem anderen
Raster-Koordinatensystem. Oder dynamisch, abhängig vom vorigen Zeichen.)
- Möglichst kleine Würfel verwenden, z.B. 2*2*2 Zeichen. Das zerhackt Texte
besser und ergibt mehr Verschlüsselungsstufen.
- Auf jeder Verschlüsselungsstufe (oder gar in verschiedenen Bereichen
derselben Stufe) andere Verfahren verwenden (andere Numerierung
der Felder, evtl. andere Formen: Rechtecke, Dreiecke, Treppen).
- Das Verfahren so auslegen, daß Worte völlig zerstreut werden: So vermeidet
man statistische Buchstabenhäufigkeiten (z.B. Endsilbe -heit), die zur
Decodierung benutzt werden können. Beispiel: Zerlegt man einen Textwürfel
zunächst senkrecht in quadratische Scheiben der Breite 1, Höhe 3, senkr. Tiefe 3,
so liegt jeder Buchstabe eines Wortes in einer anderen Scheibe (außer
wenn das Wort länger ist als die Zeile).
- Ähnlich kann man Worte zerlegen, indem man zwischen je 2 Buchstaben
mindestens ein unbenutztes Zeichen einschiebt (z.B. Zeichen des ASCII-
Codes, die in normalen Texten nicht vorkommen). Der Empfänger, der diese
Zeichen kennt, kann sie ausfiltern, ohne das genaue Verfahren zu kennen,
nach dem sie eingestreut werden.
- Auf Bitebene arbeiten: Ersetzt man jedes Zeichen im Textwürfel durch
einen Würfel von 2*2*2 = 8 Bits, so kann man das Koordinatensystem
so definieren, daß beim "Auslesen" des Gesamtwürfels diese Bitwürfel
zerlegt werden. D.h. die Bits eines Zeichens werden vor dem Verwürfeln
teilweise getrennt, gleichzeitig aber mit einigen Bits anderer
Zeichen zusammengefaßt. (Verwendet man für 1 Zeichen 3*3*3 Bits
oder mehr, mit mehreren Bitkombinationen für dasselbe Zeichen,
so verstärkt das die Kryptographie enorm).
- Code regelmäßig ändern
- Das beste Kryptographieverfahren ist sinnlos, wenn der Computer
beim Kryptographieren abgehört wird (was zumindest bis in einige 100 Meter
Entfernung möglich ist) oder das Programm während eines Internetzugangs
ausgelesen wird.
- Nie glauben, daß ein Text unentschlüsselbar ist.
Vermutlich kann auch ein Heimanwender mit einem solchen Programm, dessen
Einstellungen er selbst vornimmt, z.B. seine Mails so verschlüsseln,
daß nicht einmal Geheimdienste sie mit vertretbarem Aufwand knacken können.
Das hat natürlich 2 Seiten, aber da das Privatleben des Durchschnittsmenschen
noch nie so der Bespitzelung ausgesetzt war wie heute, ist das auch
ein Schritt zu mehr Freiheit vom großen Bruder.
Allerdings müßte auch der Empfänger den Aufwand zur Entschlüsselung treiben
(und die Programmeinstellungen kennen).
Verwendung: Religion, Philosophie
Man kann ein Rasterkoordinatensystem als Weltmodell betrachten.
(Ein ebenes Modell ist leicht vorstellbar, deshalb oft vorzuziehen).
Der Nullpunkt des ganzen Systems, bzw. die lokalen Nullpunkte,
wären dann die "Kanäle", die Verbindung zu höheren bzw. umfassenderen Ebenen.
Rasterkoordinaten als Weltmodell sind eher "föderalistisch",
Kartesische und Polarkoordinaten dagegen eher "zentralistisch".
Es wäre aber ein krasser Fehler, ein Koordinatensystem nach
ideologischen Gesichtspunkten auszusuchen.
Es muß für den jeweiligen Zweck geeignet sein.
Historisches
Es gibt Hinweise darauf, daß Raster-Koordinaten in Mysterienbünden
und Mönchsorden seit der Antike bekannt sind:
- die Zahl 9: sie stellt eine Spirale dar, was daran erinnert, daß 9
Quadrate spiralig durchlaufen werden.
- der Buchstabe g / G: erinnert genauso an eine Spirale. Trägt man das ABC
in einen Würfel ein, beginnend mit dem Buchstaben o (der der Null sehr ähnelt)
in der Mitte der untersten Ebene, so steht in der Mitte der obersten Ebene
das g (das der 9 ähnelt)! In der Mitte der mittleren Ebene steht x, was an einen
Kreuzungsmittelpunkt erinnert. An der Stelle des Leerzeichens neben dem g
käme wieder der Buchstabe o, der wegen der Ähnlichkeit zur Ziffer 0
sinnigerweise mit dem Leerzeichen assoziiert werden kann (0 = leer)
r s t a b c j k l
q o u z x d i g m
p w v y f e h n
Bemerkenswert auch die Tatsache, daß das internationale Latein-ABC
(26 Buchstaben + Leerzeichen) gerade einen 3*3*3 Würfel (also 27 Felder)
füllt. Man kann so leicht jede Position im Raum angeben.
- Auch griechische Mäander-Ornamente kann man mit einem Weg im Quadratraster
assozieren, der spiralig nach innen führt, in stets neue Quadrate.
- Mandalas: es gibt sie im Buddhismus und Hinduismus, auch in australischen,
amerikanischen und anderswo entstandenen Religionen. Auch manche
Tempelgrundrisse und gotische Rosetten sind ein Mandala. Buddhistische Mandalas
(z.B. das Anuttara Yoga-Mandala und das Vajrakila-Mandala) bestehen
oft aus verschachtelten Kreisen und Quadraten, zwischen denen spiralige
Muster vorkommen.
Man kann sicher sein, daß diese Mandalas keine grafischen Spielereien sind,
auch keine rein allegorische Weltdarstellung, sondern eher eine gemalte,
(auch mathematisch) systematisierte Weltvorstellung: vermutlich haben
Mystiker im entrückten Zustand die Welt oder Teile davon
so ähnlich gesehen. (Auch in der keltischen Kunst vorkommende Fraktal-ähnliche
Ornamente mit sich ständig wiederholenden Figuren, um menschliche Köpfe gewunden,
deuten auf eine solche innere Schau.)
Diese Erfahrungen wurden dann rational verarbeitet und systematisiert,
auch mathematisch / geometrisch. (Tatsächlich passen ja zu Chaos-Vorgängen
und Fraktalen, die in der Natur häufig sind, Rasterkoordinatensysteme besser
als übliche Koordinatensysteme.) Denn besonders im Hinduismus, dessen Weltbild
der Buddhismus teilweise übernahm, waren ja Mathematik, Geometrie und Logik
hoch entwickelt. Beispiel:
Im Buddhismus gibt es die heilige Zahl 108 , die sehr systematisch ist:
108 = 11 * 22 * 33
108 hat 12 Teiler, nämlich alle Kombinationen obiger Potenzen:
1, 2, 3, 4, 6, 9, 12, 18, 36, 27, 54, 108
108 entspricht im Iris-Koordinatensystem
einer Vierteilung des Innenkreises und
3 weiteren Ringen mit fortlaufender Dreiteilung, also 4*3*3*3 = 108 Segmenten
im äußersten Ring. (Gesamtzahl Segmente in diesen 4 Ringen:
4 + 12 + 36 + 108 = 160 = 16*10 = 25 * 5 )
108 entspricht im Vierersystem der Zahl 1230 (1*64 + 2*16 + 3*4 + 0*1)
1230 erinnert an eine öfter im Buddhismus dargestellte Handhaltung:
Linke Hand aufgerichtet, Rückansicht, linke 3 Finger leicht gespreizt,
Zeigefinger und Daumen formen eine 0 . Die Finger 1-3, die v.l.n.r immer
länger werden, entsprechen der Ziffernfolge 1-3, das Loch symbolisiert die Null,
die ganze Hand formt also die Zahl 1230 im Vierersystem (Hand = 4-Finger-Block).
Auch gilt 112304 = 36410 = Zahl der Tage im Jahr - 1
108 entspricht im Zweiersystem der Zahl 1101100. Diese läßt sich
symmetrisieren
zu 001101100. Sie enthält fast alle Teiler (außer 9, 16, 36) als Dualzahl, z.B.
112 = 3, 110112 = 33 = 27
- Tempelgrundrisse: Der (ursprünglich brahmanische, später buddhistische)
Tempel von Angkor Wat, der laut Buch allegorisch die Erschaffung der
Welt darstellt, besteht aus 3 geschachtelten, quadratischen Anlagen mit
Grünflächen dazwischen. Das innerste Quadrat hat innen ein kreuzförmiges
Muster (ähnlich der Windows-Flagge). Darin könnte man eine Anspielung
sehen auf das im Anhang beschriebene Vier-Quadrat-Raster-Koordinatensystem,
das den vollständigen Zahlenraum repräsentiert.
Rasterkoordinaten als Formales System
Man kann Rasterkoordinaten auch als mathematisches Formales System
(Kalkül) ansehen:
- Zeichenvorrat: Quadrate
- Startsymbol ist das Urquadrat 0
- Ableitungsregel 1 (nach außen): Ein Quadrat läßt sich
durch Herumlegen von 8 gleichen Quadraten zu einem
Neunerblock ergänzen.
- Ableitungsregel 2 (nach innen): Ein Quadrat läßt sich
in einen Neunerblock unterteilen.
Anhang: Variationen des Raster-Koordinatensystems
Die Benutzung der hier beschriebenen Mechanismen ist frei
Homepage




